I am a strong proponent of Julia as a programming language for scientific computing. Julia is a new language that is as fast as C/Fortran and as easy to use as Python. In this demonstration, I wrote a one-dimensional hydrodynamics code using the Lax scheme and Euler method. Below is an animation of the gas with a classical initial condition: a Sod shock tube. The simulation, plotting, and animation are all done by a single Julia script which you can download from here. The script is also copied below. From the scripts, you can appreciate the simplicity and cleanness of the syntax.

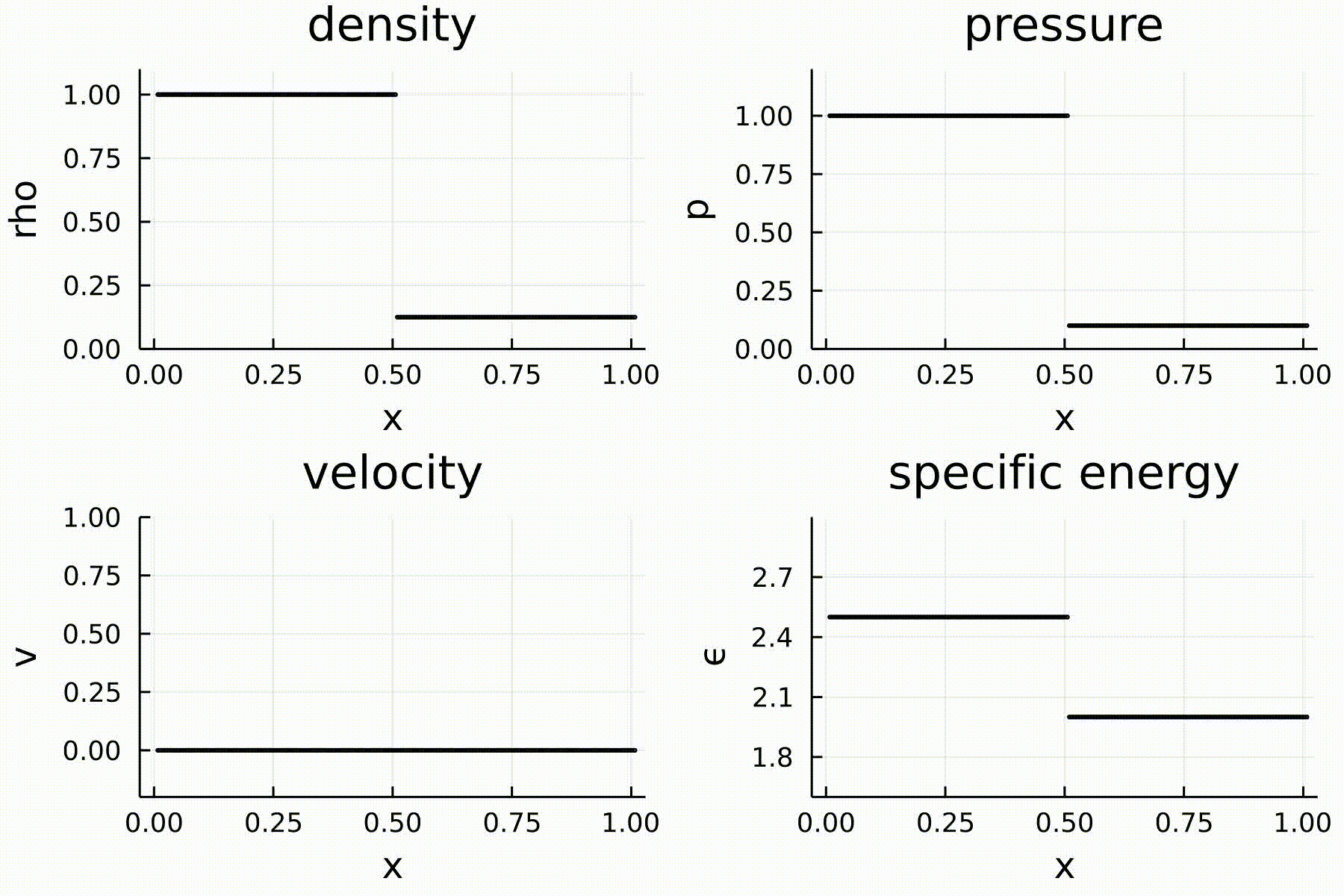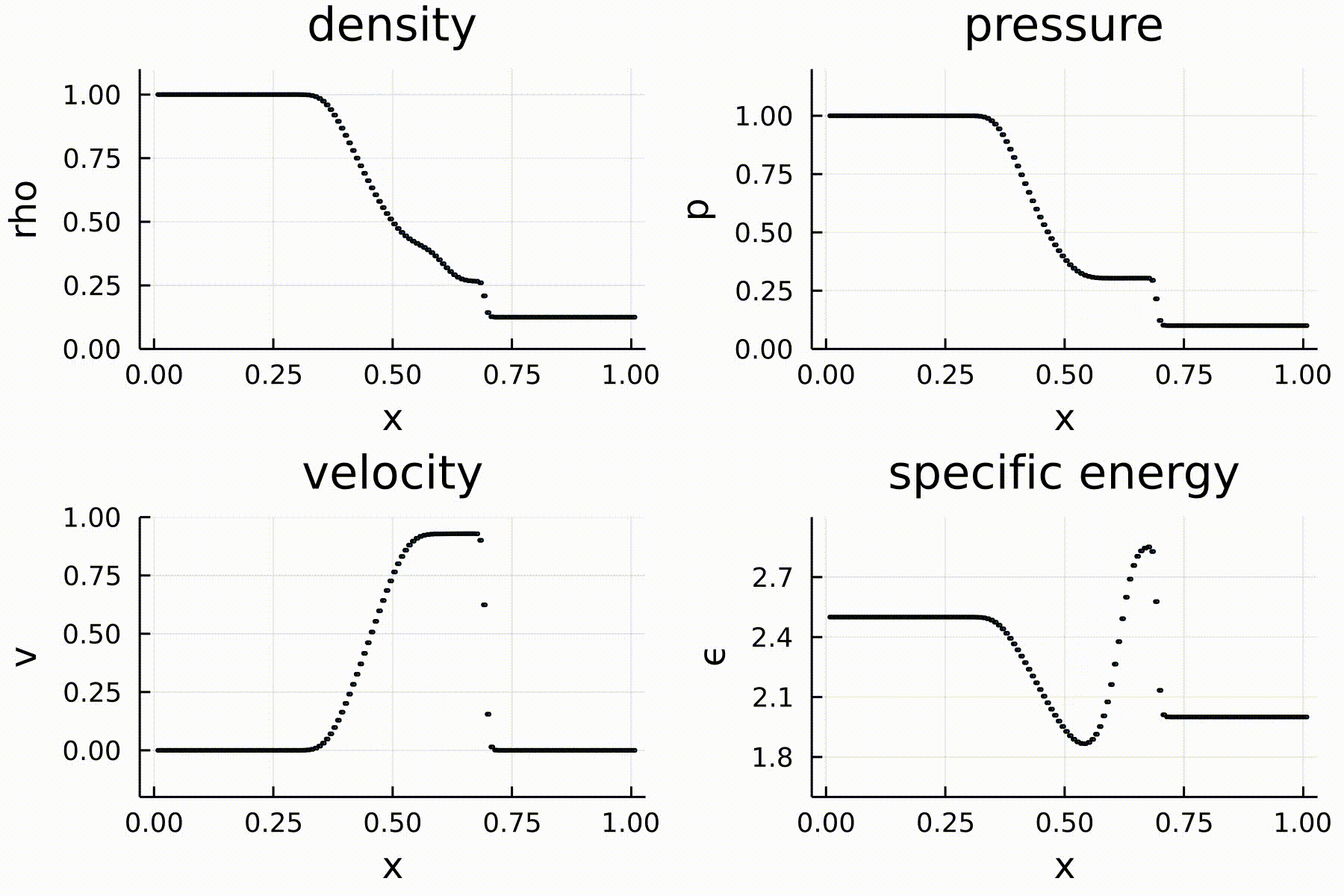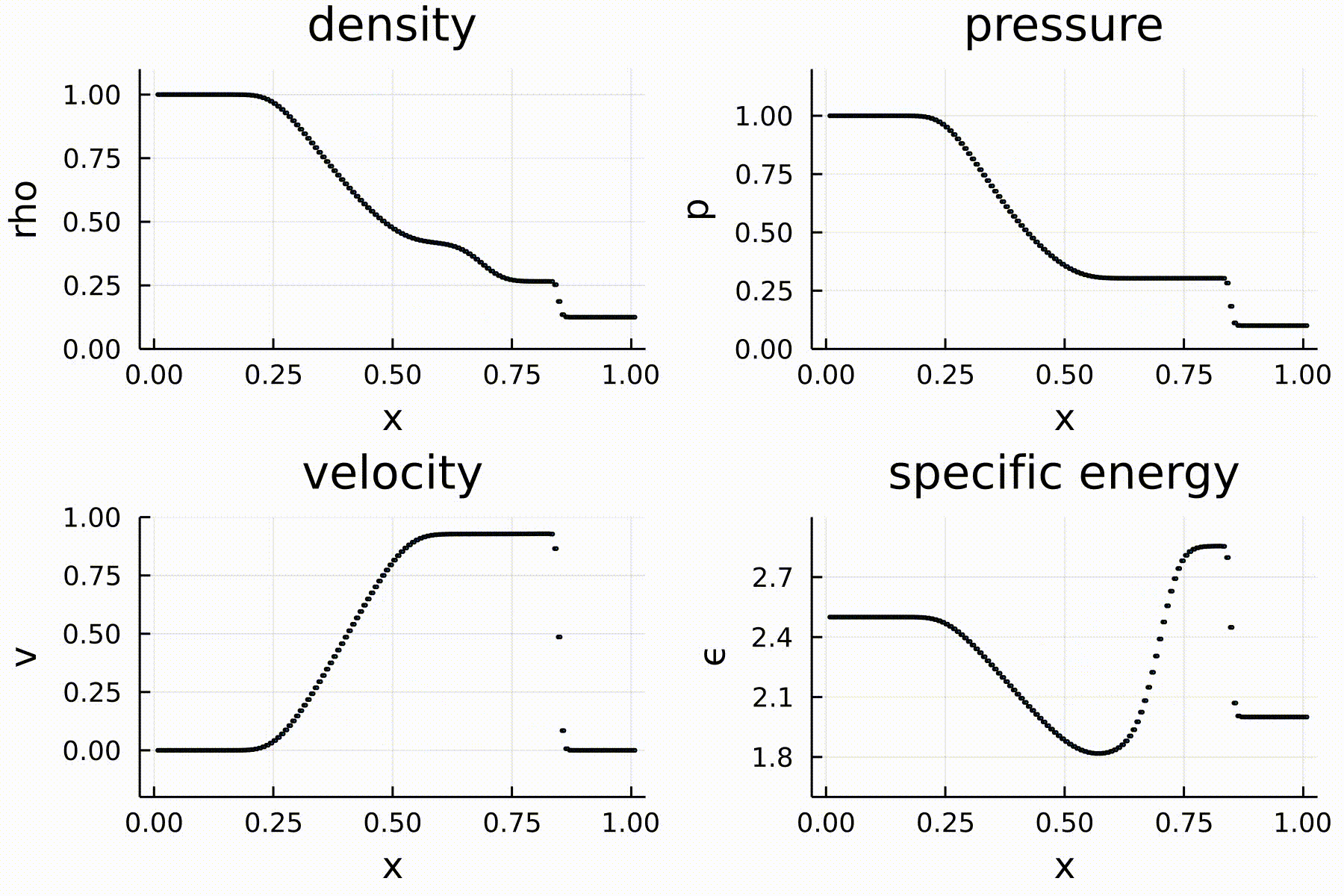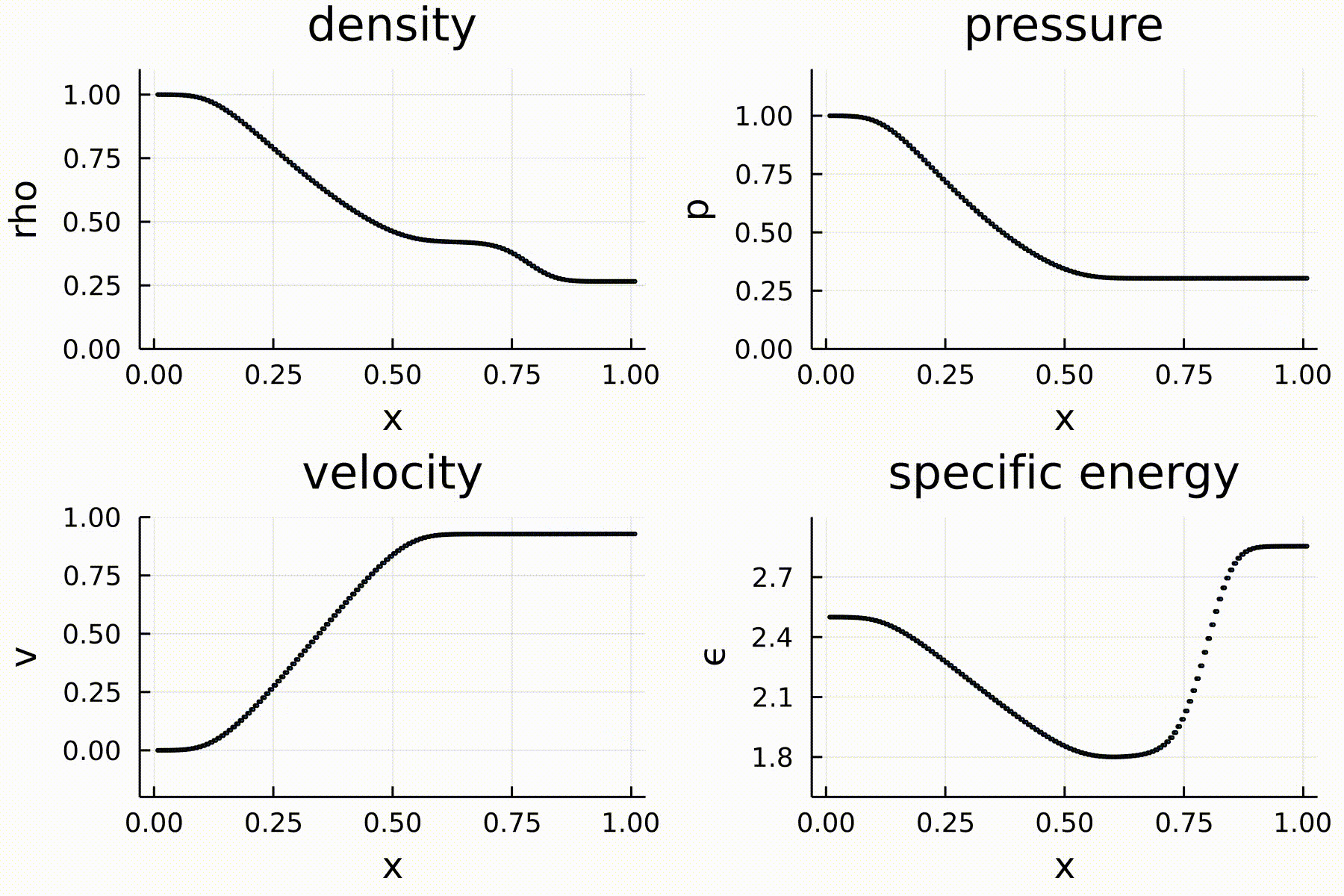
The code:

using Parameters 
using Plots
using Printf

""" A struct to store all parameters and data of the grids """
@with_kw mutable struct Grid
	nx::Int
	ng::Int
	t = 0.
	xmin = 0.
	xmax = 1.
	xlen = nx + 2 * ng
	gamma = 1.4
	jlo = ng + 1
	jhi = nx + ng
	# the grids
	dx = (xmax - xmin) / (nx - 1)
	x = xmin .+ (1:(nx + 2*ng) .- ng) * dx
	u = zeros(xlen, 3)
end

""" set the initial conditions """
function init!(g::Grid)
	mid = floor(Int16, g.xlen/2)
	g.u[1:mid, 1] .= 1.0
	g.u[(mid+1):end, 1] .= .125
	pressure = zeros(Float64, g.xlen)
	pressure[1:mid] .= 1.0
	pressure[(mid+1):end] .= 0.1
	g.u[:, 2] .= 0.
	g.u[:, 3] .= pressure ./ (g.gamma - 1)
	return
end

function flux(g::Grid)
	pressure = @. (g.gamma - 1) * (g.u[:, 3] - 0.5 * g.u[:, 2]^2 / g.u[:, 1])
	fu = zeros(Float64, g.xlen, 3)
	@. fu[:, 1] = g.u[:, 2]
	@. fu[:, 2] = g.u[:, 2]^2 / g.u[:, 1] + pressure
	@. fu[:, 3] = (g.u[:, 3] + pressure) * g.u[:, 2] / g.u[:, 1]
	return fu
end

function fill_BCs!(g::Grid)
	for k = 1:3, i = 1:g.ng
		g.u[i, k] = g.u[g.jlo, k]
		g.u[g.jhi+i, k] = g.u[g.jhi, k]
	end
	return
end

""" make the plot or update the animation """
function plot_curve(g::Grid; fn="t.png")
	# calculate rho, u, p e
	x = g.x[g.jlo:g.jhi]
	rho_f = g.u[g.jlo:g.jhi, 1]
	vel_f = g.u[g.jlo:g.jhi, 2] ./ rho_f
	e_f  = g.u[g.jlo:g.jhi, 3]
	epsilon_f = @. (e_f / rho_f) - (0.5 * vel_f^2)
	p = @. (g.gamma - 1) * rho_f * epsilon_f
	data = zeros(size(rho_f, 1), 4)
	data[:, 1] .= rho_f
	data[:, 2] .= p
	data[:, 3] .= vel_f
	data[:, 4] .= epsilon_f
	scatter(x, data, layout=4,
			title=["density" "pressure" "velocity" "specific energy"],
			ms=1, legend=false, xlabel="x", ylabel=["rho" "p" "v" "ϵ"],
			xlim=[0, 1], ylim=[(0., 1.1) (-0., 1.2) (-.2, 1) (1.6, 3.)], dpi=300)
	savefig(fn)
end

""" the main function """
function main(dx, tmax; dnout::Int=1)
	g = Grid(nx=dx, ng=1, t=0.)
	v = 1.
	C = 0.45
	dt = C * g.dx / v
	init!(g)
	unew = similar(g.u)
	count = 0
	ocount = 0
	fn = @sprintf("fig/f_%04d.png", ocount)
	plot_curve(g, fn=fn)
	println("$(fn), t = $(g.t)")
	while g.t < tmax + dt - 1e-10
		if g.t > tmax
			g.t = tmax
			dt = dt - (g.t - tmax)
		end
		count += 1
		### LAX SCHEME ###
		fill_BCs!(g)
		fu = flux(g)
		for k = 1:3, j = g.jlo:g.jhi
			unew[j, k] = 0.5 * (g.u[j - 1, k] + g.u[j + 1, k]) -
				0.5 * dt / g.dx * (fu[j + 1, k] - fu[j - 1, k])
		end
		g.u = copy(unew)
		g.t += dt
		if count % dnout == 0
			ocount += 1
			fn = @sprintf("fig/f_%04d.png", ocount)
			plot_curve(g, fn=fn)
			println("$(fn), t = $(g.t)")
		end
	end
end 

run(`mkdir -p fig`)
tend = 0.3
main(256, tend, dnout=10)
# uncomment the following line to create a animation
# run(`ffmpeg -r 10 -f image2 -i fig/f_%04d.png -vcodec mpeg4 -b 10M animation.avi`)